오답노트
푸리에 변환(fourier transfrom) 본문
푸리에 변환은 시간과 공간에 대한 함수를 시간 또는 공간 주파수에 대한 성분으로 분해하여 변환한다.
즉, 어떤 개체를 분석하여 그 개체를 이루고 있는 파동들을 분석하는 것
시간 x 진폭의 형태의 2d 오디오 파일 그래프를 주파수 x 진폭의 형태로 바꿔준다.
시간순으로 나열 된 진폭 안에 담겨있는 주파수를 확인하기 위한 방법이다.
결국 오디오 신호라는 것은 시간에 따라 무엇인가가 변화하였다는 것을 뜻하는데 이 푸리에변환을 이용하면 그 연속적인 신호 안에서 개개인의 신호를 추출 할 수 있다.
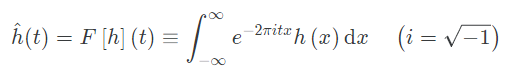
위의 그림은 푸리에 변환 공식이다.
import librosa
import numpy as np
y, sr = librosa.load('filepath')
ft = np.fft.fft(y)
ft = np.abs(ft)
코드는 위와 같이 필요 오디오 파일을 로드 한 뒤 Numpy 에서 제공하는 모듈로 변환시키면 된다.
저 코드를 풀어서 쓰면 아래와 같이 표현 할 수 있는데,
def fftnoise(f):
f = np.array(f, dtype = 'complex') # dtype 복소수형태의 arr 생성
Np = (len(f) - 1) // 2
phase = np.random.randn(Np) * 2 * np.pi # 지름이 2 인 반지름을 감는 난수 생성
phase = np.cos(phase) + 1j * np.sin(phase) # 복소평면에서의 시간 정의
f[1 : Np + 1] *= phase
f[-1 : -1 - Np : -1] = np.conj(f[1 : Np + 1])
return np.fft.fft(f).real # 위 코드를 통해 나온 값의 실수값만 반환
정의 된 함수를 보면 복소수형태의 array 와 삼각함수 등이 나온다.
위의 코드를 해석하기 위해선 아래의 영상을 참고하면 될 듯 하다. (아직 완전히 이해하지는 못 했다.)
우리가 듣고 있는 소리의 파형은 사실 여러개의 주파수가 겹친 합성 주파수의 영역인데,
이를 복수평면에 넣어 한 바퀴를 돌 때 신호의 무게중심을 파악하여 그래프를 그리게 된다.
이 때, 무게중심의 그래프에서 가끔씩 튀는 부분이 생기게 되는데 이 부분을 따로 추출하게 되면 특정 주파수를 알 수 있다.
어려운 말이나 개념은 차치하고서라도 인풋 데이터를 진폭을 시간순으로 나열한 데이터로 넣으면 아웃풋 데이터는 진폭을 주파수 순으로 나열한 데이터가 나오게 된다.
이를 통해 해당 오디오 파일에는 주파수가 어느 정도의 세기로 존재하는가를 알 수 있다.
import matplotlib.pyplot as plt
fig = plt.figure(figsize = (16, 6))
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
librosa.display.waveplot(y, sr = sr, ax = ax1)
librosa.display.waveplot(ft, sr = sr, ax = ax2)
fig.tighit_layout()
plt.show()

위 사진을 보게 되면 y 축이 바뀐 것을 확인할 수 있다.
원본 데이터인 위의 경우 amplitude 값이며 fft 를 거친 데이터인 아래의 경우 y 축이 frequency 가 되었다.
위의 경우는 수학적으로 풀이를 한 코드이고, 좀 더 쉽게 풀이를 해보자면 아래와 같다.
import numpy as np
import librosa
import librosa.display
import matplotlib.pyplot as plt
y, sr = librosa.load(
'filepath'
) # 원본 오디오 파일을 로드한다
ft = np.fft.fft(y) # fft 변환 : 복소수 형태의 len(y) 의 길이별로 나온다
ft = abs(ft) # 복소수 형태의 배열 중 실수 부분만 추출한다
# visualization
plt.figure(figsize = (16, 6))
plt.plot(ft) # fft 한 형태를 그래프로 시각화한다
plt.tight_layout()
plt.show()
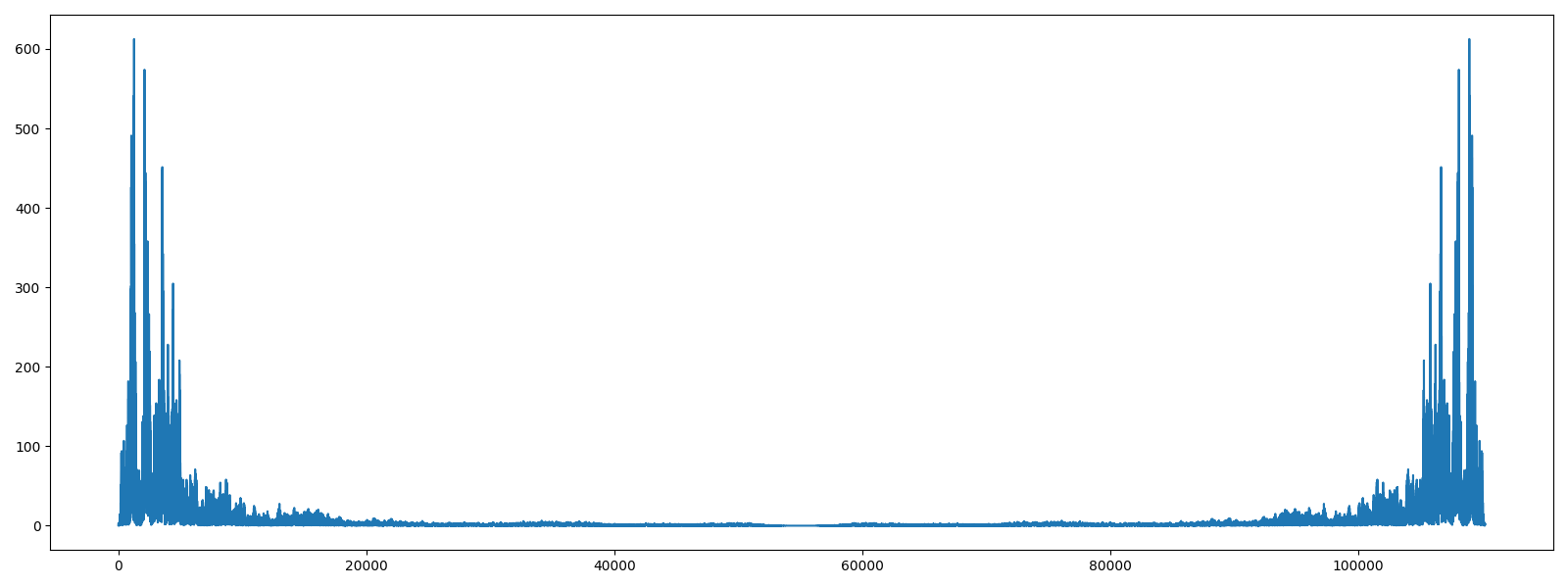
보면 양옆으로 길게 늘어져있는 것을 확인할 수 있는데, 이는 fft 를 실시할 때 이산 푸리에 변환 (DFT) 이라는 것을 사용하기 때문이라고 한다. 자세한 내용은 추후에 좀 더 공부한 뒤 적어놓도록 하겠으며, 그래프는 가운데 (5만 언저리) 를 기준으로 양 옆으로 같은 모양을 하고 있는데, 이를 좀 더 쉽게 보기 위해서는 아래와 같이 fft.fftfreq() 를 사용한다.
fr = np.fft.fftfreq(len(y), d = 1.0)
# 시각화 하는 데에 있어 주파수가 필요하므로 numpy 에서 제공하는 툴을 쓴다.
plt.figure(figsize = (16, 6)) # 시각화 그래프 사이즈
plt.xlim(0, 0.7) # x 축의 범위를 0부터 시작하도록 제한시킨다
plt.ylim(0, 700) # t 축의 범위를 0부터 700까지로 제한시킨다
plt.plot(fr, ft)
plt.show()
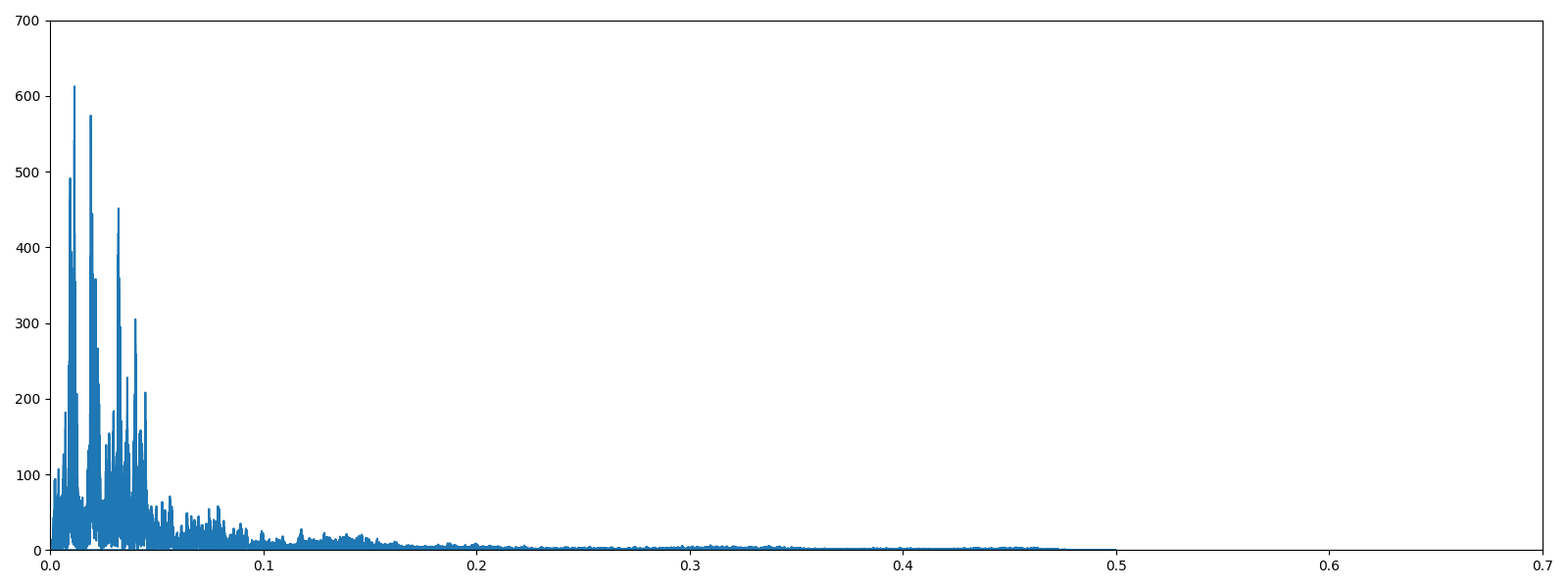
위에서 보면 우리가 많이 봤던 fft 그래프가 완성 되었다.
아까 위의 영상을 봤다면 (안 봤더라도) 알 수 있는 것이 해당 그래프에서 위로 솟구치고 있는 것들이 특정 주파수의 영역인 셈이다. 즉, 위로 올라와있는 한 개의 점마다 특정 주파수가 있다는 뜻이며, 해당 오디오 파일은 그런 특정 주파수들의 합성 신호라고 볼 수 있다.
저 그래프에서 각 시간대별로 잘라 주파수를 특정하는 것을 stft (short term fourier transform) 이라고 한다.
'프로젝트 > 화자 구분 음성 기록' 카테고리의 다른 글
| 화자구분 (남녀) 모델 - CNN (0) | 2021.04.22 |
|---|---|
| denoise (0) | 2021.04.22 |
| librosa parameter 분석 : mfcc_to_audio (0) | 2021.04.03 |
| librosa parameter 분석 : mfcc_to_mel_2 (0) | 2021.04.03 |
| librosa parameter 분석 : mfcc_to_mel_1 (0) | 2021.04.03 |


